
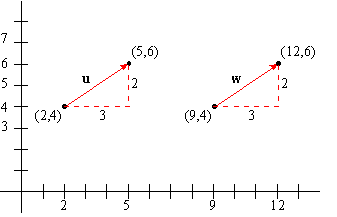

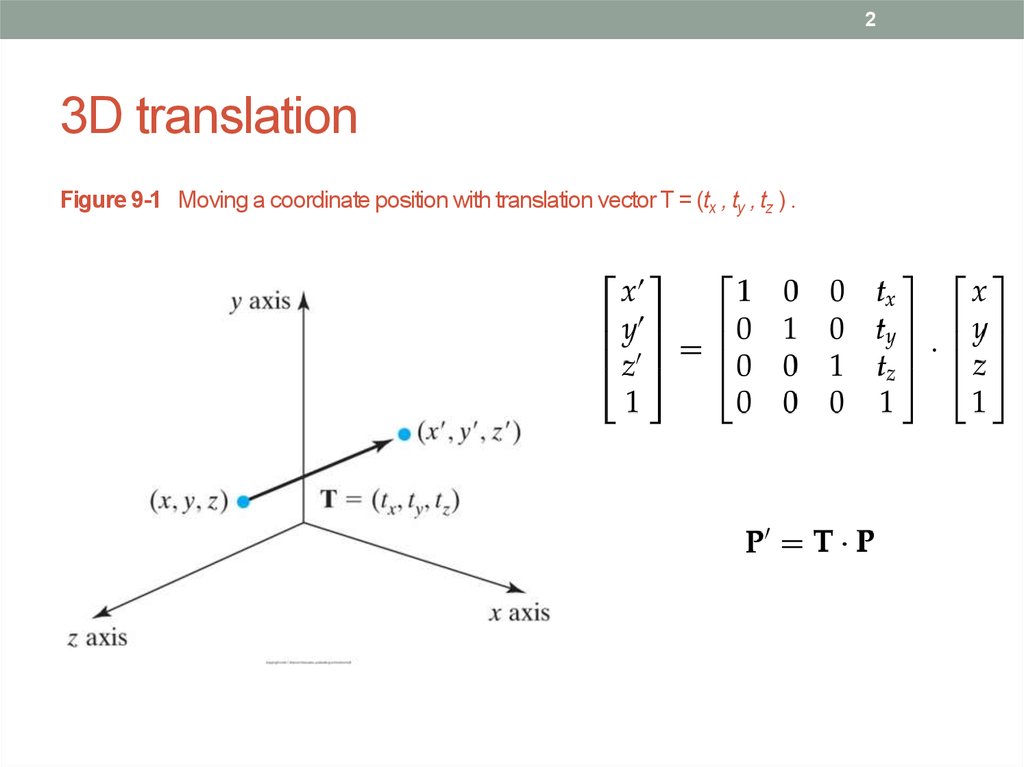
x 1 + 3 x 2 + 3 x 3 + 3 x 4 + 3 y 1 + 2 y 2 + 2 y 2 + 2 y 2 + 2 If we want to dilate a figure we simply multiply each x- and y-coordinate with the scale factor we want to dilate with. Sway, translation along the transverse axis (from side to side) We can use matrices to translate our figure, if we want to translate the figure x+3 and y+2 we simply add 3 to each x-coordinate and 2 to each y-coordinate.Surge, translation along the longitudinal axis (forward or backwards).A common example is a periodic function, which is an eigenfunction of a translation operator.įor describing vehicle dynamics (or movement of any rigid body), including ship dynamics and aircraft dynamics, it is common to use a mechanical model consisting of six degrees of freedom, which includes translations along three reference axes, as well as rotations about those three axes. Translational symmetry Main page: Translational symmetryĪn object that looks the same before and after translation is said to have translational symmetry. The passive version of an active geometric translation is known as a translation of axes. While geometric translation is often viewed as an active process that changes the position of a geometric object, a similar result can be achieved by a passive transformation that moves the coordinate system itself but leaves the object fixed. Translation of axes Main page: Translation of axes If \displaystyleīecause addition of vectors is commutative, multiplication of translation matrices is therefore also commutative (unlike multiplication of arbitrary matrices). 1.1 Horizontal and vertical translations.


 0 kommentar(er)
0 kommentar(er)
